The Trouble With Ringworlds

Hard science fiction writers play by the rule that for the most part their stories should not violate the known laws of physics. This still gives plenty of latitude. Thus cosmic scale engineering, though not feasible at our level of technology, is allowed. One of the more gigantic cosmic constructs was proposed by the physicist Freeman Dyson. In the search for extraterrestrial intelligence, Dyson suggests we should look for large infra red sources. The rational is that an advanced civilization would make use of the entire energy output of its star. Hence it would surround the star with a shell that would intercept all the emitted radiation. Dyson's idea has been misinterpreted by most science fiction writers, including the writers of the Star Trek scripts. They literally interpret the Dyson sphere as a solid shell, with the inhabitants living on its inside. Dyson's idea is impressive enough, his thinking being that the star would eventually be surround by so many space habitats that essentially none of its radiation would be able to escape. In either case the only indication of the star's presence would be the infra red re-radiation of its energy output.


The SF writer, Larry Niven, proposed an impressive variant of the Dyson sphere, suggesting that a rotating ring be constructed around the star. In his book, "Ring World", the ring spins about the star fast enough to provide enough centrifugal force to simulate the gravity of an earth like planet. Thousand mile high walls on the edges of the ring are used to retain the atmosphere. The resulting living area is vast and provides a nice background for his characters to roam around.

But hard core SF writers have to live with their fans, and Niven's quickly pointed out that his ring world was unstable, if slightly perturbed it would move off center and the edge would collide with the central star. It takes a fair amount of mechanics and math to show this, but this was no obstacle to many of his readers.

Of course being a creative author, Niven turned his error into a plot element for the next book, "The Ringworld Engineers".

What I would like to show here is that an elementary knowledge of Newtonian principles can show why the Ringworld is unstable. All we need know is that gravitational force falls off as the inverse square of distance and that the velocity of body su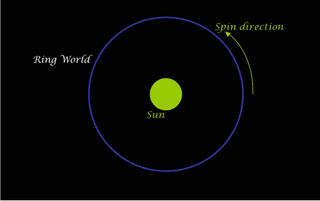ch as a planet in orbit about its star becomes smaller as the distance from the star increases. Thus the orbital velocity of the Earth is much higher than the orbital velocity of Mars.
The first figure shows the basic configuration of the Ringworld rotating about its star. The spin of the Ringworld also maintains the orientation by the principal of conservation of angular momentum.

In the next figure the Ringworld is displaced with the star no longer in the center. The figure actually shows both the original position and the displaced position. The arrows indicate the orbital velocity of a body at the given distance from the star. The "a" arrows show the velocity needed to maintain orbit. This is the classic situation that the acceleration of gravity is countered by the tangential velocity of the orbiting object, which is the Newtonian explanation of why the moon doesn't fall down! The upper "b" arrow is the orbital velocity needed at the displaced position, which is closer to the star. Similarly the lower "c" arrow is the orbital velocity needed at the greater distance from the star. In the upper case this means that the tangential spin velocity will be too small for maintaining orbit, that the gravitational force will move this part of the Ringworld toward the star. In the case of the lower position, now further from the star, the velocity will be too great to maintain orbit, hence this part of the Ringworld will move further away from the star. The net result is that what starts out as a small displacement will tend to increase, which is the essence of instability.

The last two figures show what happens if there is no rotation and we just consider the force of gravity. The arrows just indicate the force of gravity on the various portions of the Ringworld, taking into account the inverse square law. Clearly this is an unstable situation.
Off course this arguments are only approximate as the Ringworld is postulated to be a continuous object. If we go back to Dyson's original idea, the Ringworld would be a discontinuous cloud of space habitats and there would be no stability problem. The Dyson Spheres of Science Fiction are another matter.

Even so, as a setting for a science fiction story, Niven's Ringworld is a lot more interesting. If you want to find out how he deals with the stability problem you'll have to read the book!

Cheers,
Marty